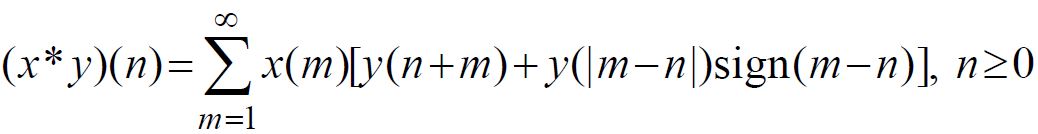SAITOH TYPE DISCRETE INEQUALITY FOR THE DISCRETE-TIME FOURIER COSINE GENERALIZED CONVOLUTION

Nguyen Anh Dai; Nguyen Thi Huong Giang; Dang Van Tien

Nguyen Anh Dai Hung Yen University of Technology and Education
Nguyen Thi Huong Giang Hung Yen University of Technology and Education
Dang Van Tien Hung Yen University of Technology and Education

Keywords: Discrete convolution, discrete Saitoh type inequality, discrete-time Fourier cosine transform, Parseval theorem

Abstract

Discrete-time Fourier cosine generalized convolution of sequences x(n) and y(n) in the form

is studied. In this paper, we consider the Parseval’s theorem and the discrete Saitoh’s inequality.

References

S. Saitoh, Some inequalities for analytic functions with a finite Dirichlet integral on the unit disc, Math. Ann., 1979, 246, pp. 69–77.

S. Saitoh, Some inequalities for entire function, Proc. Amer. Math. Soc., 1980, 80, pp. 254–258.

S. Saitoh, Weighted Lp-norm inequalities in convolution, Survey on Classical Inequalities, Kluwer Academic Pulishers, Amsterdam, 2000, pp. 225–234.

N. Aronszajn, Theory of reproducing kernels, Trans. Amer. Math. Soc., 1950, 68, pp. 337–404.

S. Saitoh, Integral transforms, reproducing kernels and their applications, Pitman researchnotes in mathematics series 369, 1997, Addison Wesley Longman, UK.

N.H.V. Nhan, D.T. Duc, V.K. Tuan and N.H.V. Vu, Inequalities for differences and their applications, Jour. Diff. Equa. & Appl., 2014, 20, pp. 1319-1343.

J. Burbea, A Dirichlet norm inequality and some inequalities for reproducing kernel spaces, Proc. Amer. Math. Soc., 1981, 83, pp. 279–285.

J. Burbea, Norm inequalities of exponential type for holomorphic functions, Kodai Math. J., 1982, 5, pp. 339–354.

M. Cwikel and R. Kerman, On a convolution inequality of Saitoh, Proc. Amer. Math. Soc., 1996, 124, pp. 773–777.

K. F. Andersen, Weighted inequalities for iterated convolutions, Proc. Amer. Math. Soc., 1999, 127, pp. 2643–2651.

S. Saitoh, V. K. Tuan and M. Yamamoto, Convolution inequalities and applications, J. of Ineq. in Pure & Appl. Math., 2003, 4, pp. 1-8.

S. Saitoh, V. K. Tuan and M. Yamamoto, Reverse weighted Lp-norm inequalities inconvolutions and stability in inverse problems, J. of Ineq. in Pure & Appl. Math., 2000, 1, pp. 1-7.

N.X. Thao and N.A. Dai, Discrete-time Fourier sine integral transform, Jour. Math. App., 2018, 16, pp. 51-62.

N.A. Dai and N.X. Thao, Generalized convolutions with weight-function for discrete-time Fourier cosine and sine transforms, Annales Univ. Sci. Budapest., Sect. Comp., 2018, 47, pp. 227-237.

N.X. Thao, V.K. Tuan and N.A. Dai, Discrete-time Fourier cosine convolution, Int. Trans. & Spec. Funct., 2018, 29, pp. 866-874.

N.X. Thao, V.K. Tuan and N.A. Dai, A discrete convolution involving Fourier sine and cosine series and its applications, Int. Tran. & Spec. Func., 2020, 31, pp. 243-252.

A.V. Oppenheim and R.W. Schafer, Discrete-Time Signal Processing, 1989, Prentice Hall, Englewood Cliffs.

A.D. Poularikas, Transforms and Applications, 3rd ed., 2010, NewYork CRC Press.

R.K. Rao Yarlagadda, Analog and Digital Signal and Systems, DOI: 10.1007/9781441900340, Springer Science - Business Media, LLC 2010.