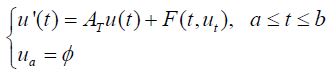COMPACTNESS OF SOLUTION SEMIFLOWS WITH FINITE DELAY
Abstract
In this paper, we prove the compactness of solutions of semilinear differential equations of the form
under the conditions that the operator T A generates the strongly continuous operators semigruops (T(t)) t≥0 and the nonlinear term satisfying the Lipschitz condition. The main results are based on the method using
norm evaluations and the compactness of the operator in the corresponding Banach space.
References
J. Hadamard, “Sur l’intération et les solutions asymptotiques des equations différentielles”. Bulletin de la Société Mathématique de France, 1901, 29, pp. 224-228.
O. Perron, “Uber stabilitat und asymptotisches verhalten der integrale von differentialgleichungssystemen”. Mathematische Zeitschrift, 1929, 29, pp. 129-160.
O. Perron, “Die stabilitatsfrage bei differentialgleichungen”. Mathematische Zeitschrift, 1930, 32, pp. 703-728.
N. Bogoliubov, Yu. Mitropolsky, “The method of integral manifolds in nonlinear mechanics”. Contributions to Differential Equations, 1963, 2, pp. 123-196.
N. Bogoliubov, Yu. Mitropolsky, Asymptotic Methods in the Theory of Non-Linear Oscillations, 1961, Translated from the second revised Russian edition, International Monographs on Advanced Mathematics and Physics, Gordon and Breach Science Publishers, New York.
J.L. Daleckii, M.G. Krein, Stability of solutions of differential equations in Banach spaces, 1974, Translations of Mathematical Monographs, American Mathematical Society, Providence, Rhode Island.
A. Pazy, Semigroups of Linear Operators and Application to Partial Differential Equations, 1983, Springer, New York.