INVARIANT CENTER - UNSTABLE MANIFOLDS FOR PARTIAL FUNCTIONAL DELAY DIFFERENTIAL EQUATIONS
Abstract
We prove the existence of an invariant center-unstable manifold of -class for solutions to the partial functional delay differential equation of the form
u'(t) = A(t)u(t) + f(t, ut), t∈R
when its linear part, the family operators (A(t))t ∈R, generates the evolution family (U(t,s))t ≥ s having an exponential dichotomy or trichotomy on the R and the nonlinear forcing delay term f satisfies the 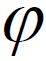
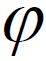
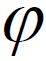
References
S. Busenberg, W. Huang, “Stability and Hopf bifurcation for a population delay model with diffusion effects”. J.Diff. Eq., 1996, 124, pp. 80-107.
J. Carr, Applications of Center Manifold Theory. Applied Mathematical Sciences, 1981, 35, Springer-Verlag,New York-Berlin.
W. Feng, X. Lu, “Asymptotic periodicity in diffusive logistic equations with discrete delays”.Nonlinear Analysis -TMA, 1996, 26, pp. 171-178.
N. T. Huy, “Exponential dichotomy of evolution equations and admissibility of function spaces on a half-line”. J.Funct. Anal., 2006, 235, pp. 330-354.
N. T. Huy, T. V. Duoc, “Integral manifolds for partial functional differential equations in admissible spaces on a half-line”. J.Math.Anal.Appl., 2014, 411, pp. 816-828.
N. T. Huy, T. V. Duoc, “Unstable manifolds for partial functional differential equations in admissible spaces on the whole line”. Vietnam J. Math., 2015, 43, pp. 37-55.
N.T. Huy, D.X. Khanh, “Local stable manifolds of admissible classes for parabolic functional equations and applications to Hutchinson models”. International Journal of Evolution Equations, 10 2017, pp. 391-406.
J. Lin, P. B. Kahn, “Phase and amplitude instability in delay diffusion population models”. J. Math. Biol., 1982, 13, pp. 383-393.
R. Nagel, G. Nickel, “Well-posedness for non-autonomous abstract Cauchy problems”. Prog. Nonl. Diff.Eq.Appl., 2002, 50, pp. 279-293.
A. Pazy, Semigroup of Linear Operators and Application to Partial Differential Equations, Springer-Verlag, Berlin, 1983.

