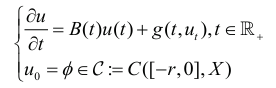INVARIANT STABLE MANIFOLDS FOR  PARTIAL FUNCTIONAL DIFFERENTIAL EQUATIONS WITH FINITE DELAY

Trinh Xuan Yen; Nguyen Thi Thu Hang

Trinh Xuan Yen Department of Basic Science, Hung Yen University of Technology and Education
Nguyen Thi Thu Hang Department of Basic Science, Hung Yen University of Technology and Education

Keywords: Banach function space, evolution family, exponential dichotomy, manifold

Abstract

We prove the existence of invarinat stable manifolds for the solutions to the equation

in the case where the evolution family (U(t,s))_t≥s≥0has an exponential dichotomy on a half-line, and the nonlinear forcing term g satisfies the 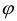-Lipschitz conditions, i.e., , where belongs to some classes of admissible function space. Our main method is based on the addmissibility of function space.

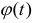
References

J. Hadamard, “Sur l’interation et les solutions asymptotiques des equations differentielles”. Bull. Soc. Math. France, 1901, 29, pp. 224-228.

O. Perron, “Uber Stabilit at und asymptotiques Verhalten der Integrale von Differential gleichungs systemen”. German Math. Z, 1929, 29, no. 1, pp. 129-160.

N.V. Minh, J. Wu, “Invariant manifolds for partial functional differential equations”. J. Differential Equations, 2004, 198, pp. 381-421.

N.T.T. Hang, T.X. Yen, “Conditions for existence of solutions for partial functional delay differential equations on a half-line”. UTEHY Joural of Science and Technology, 2023, 38, pp. 85-90.

N.T. Huy, “Invariant manifolds of admissible classes for semi-linear evolution equations”. J. Differential Equations, 2009, 246, pp. 1820-1844.

A. Pazy, Semigroup of Linear Operators and Application to Partial Differential Equations, Spinger-Verlag, Berlin, 1983.