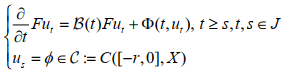THE BEHAVIOR OF SOLUTIONS TO PARTIAL NEUTRAL FUNCITONAL DIFFERENTIAL EQUATIONS

Nguyen Thi Thu Hang; Nguyen Thi Hanh

Nguyen Thi Thu Hang Department of Basic Science, Hung Yen University of Technology and Education
Nguyen Thi Hanh Department of Basic Science, Hung Yen University of Technology and Education

Keywords: Banach function spaces, evolution family, exponential dichotomy, manifold

Abstract

In this paper, we analyze the behavior of solutions to partial neutral functional differential equations

under the conditions that the family of linear operators 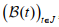, defined on a Banach space X , generates an evolution family which has an exponential dichotomy on J = ⁺or J = , and the nonlinear term Φ satisfies the -Lipschitz conditions, i.e., , where (t) belongs to some admissible function spaces. Our main method is based on the admissibility of function spaces.

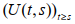
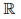
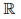
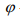
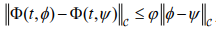
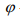
References

J. Hadamard, “Sur l’interation et les solutions asymptotiques des equations differentielles”. Bull. Soc. Math. France, 1901, 29, pp. 224-228.

O. Perron, “Uber Stabilit at und asymptotiques Verhalten der Integrale von Differential gleichungs systemen”. German Math. Z, 1929, 29, no. 1, pp. 129-160.

N.V. Minh, J. Wu, “Invariant manifolds for partial functional differential equations”. J. Differential Equations, 2004, 198, pp. 381-421.

N.T.T. Hang, T.X. Yen, “Conditions for existence of solutions for partial functional delay differential equations on a half-line”. UTEHY Joural of Science and Technology, 2023, 38, pp. 85-90.

N.T. Huy, “Invariant manifolds of admissible classes for semi-linear evolution equations”. J. Differential Equations, 2009, 246, pp. 1820-1844.

N.T. Huy, D.X. Khanh, “Local stable manifolds of admissible classes for parabolic functional equations and applications to Hutchinson models”, International Journal of Evolution Equations, 2017, 10, pp. 391-406.

A. Pazy, Semigroup of Linear Operators and Application to Partial Differential Equations, Spinger-Verlag, Berlin, 1983.

N.T. Huy and P.V. Bang, “Unstable manifolds for partial neutral differential equations and admissibility of function spaces”. Acta Mathematica Vietnamica, 2017, 42, pp. 187-207.

N.T. Huy and P.V. Bang, “Invariant stable manifolds for partial neutral differential equations in admissible spaces on a half-line”. Discrete and Continuous Dynamical Systems- Series B, 2015, 20, pp. 2993-3011.