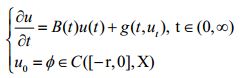CONDITIONS FOR EXISTENCE OF SOLUTIONS FOR PARTIAL FUNCTIONAL DELAY DIFFERENTIAL EQUATIONS ON A HALF-LINE
Abstract
For the following class of partial functional delay differential equations
we establish the existence and bounded conditions of solutions. In the case of its linear part, the family operators (B(t))t≥0, generates the evolution family (U(t,s))t≥s≥0 (on Banach space X) having an exponential dichotomy on the half-line and the nonlinear forcing delay term f satisfes the 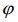
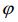
References
J. Hadamard, “Sur l’interation et les solutions asymptotiques des equations differentielles”, Bull. Soc. Math. France, 1901, 29, pp. 224-228.
O. Perron, “Uber Stabilit¨at und asymptotisches Verhalten der Integrale von Differential gleichungs systemen”. German Math. Z, 1929, 29, no. 1, pp. 129-160.
N.V. Minh, J. Wu, “Invariant manifolds of partial functional differential equations”. J. Differential Equations, 2004, 198, pp. 381 - 421.
N. T. Huy, T. V. Duoc, “Integral manifolds for partial functional differential equations in admissible spaces on a half-line”. J. Math. Anal. Appl., 2014, 411, pp. 816-828.
N.T. Huy, D.X. Khanh, “Local stable manifolds of admissible classes for parabolic functional equations and applications to Hutchinson models”, International Journal of Evolution Equations, 2017, 10, pp. 391-406.
A. Pazy, Semigroup of Linear Operators and Application to Partial Differential Equations, Springer-Verlag, Berlin, 1983.
R. Nagel, G. Nickel, “Well-posedness for non-autonomous abstract Cauchy problems”, Prog. Nonl. Diff. Eq. Appl., 2002, 50, pp. 279-293.