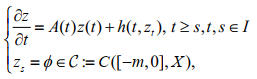RELATIONSHIP BETWEEN STABLE MANIFOLDS AND UNSTABLE MANIFOLDS FOR FINITE DELAY PARTIAL FUNCTIONAL DIFFERENTIAL

Nguyen Thi Hanh; Nguyen Thi Thu Hang

Nguyen Thi Hanh Department of Basic Science, Hung Yen University of Technology and Education
Nguyen Thi Thu Hang Department of Basic Science, Hung Yen University of Technology and Education

Abstract

Based on the equation

we construct a homomorphism from the intersection of two integral manifolds to a subspace of the phase space 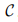. Here, the evolution family is generated by the family of linear operators in the Banach space X. The delay term h(t, z_t) satisfies the ψ-Lipschitz conditions, i.e., , where ψ(t) belongs to some classes of admissible function spaces. Our main method is based on the admissibility of function spaces.

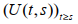
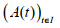
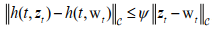
References

J. Hadamard, “Sur l’interation et les solutions asymptotiques des equations differentielles”. Bull. Soc. Math. France, 1901, 29, pp. 224-228.

O. Perron, “Uber Stabilit at und asymptotiques Verhalten der Integrale von Differential gleichungs systemen”. German Math. Z, 1929, 29, no. 1, pp. 129-160.

N.T.T. Hang, T.X. Yen, “Conditions for existence of solutions for partial functional delay differential equations on a half-line”. UTEHY Joural of Science and Technology, 2023, 38, pp. 85-90.

N.T. Huy, “Invariant manifolds of admissible classes for semi-linear evolution equations”. J. Differential Equations, 2009, 246, pp. 1820-1844.

N.T. Huy, D.X. Khanh, “Local stable manifolds of admissible classes for parabolic functional equations and applications to Hutchinson models”. International Journal of Evolution Equations, 2017, 10, pp. 391-406.

T.X.Yen, “Invariant center-unstable manifolds for partial functional delay differential equations”. UTEHY Journal of Science and Technology, 2022, 35, pp. 84-89.

T.X.Yen, N.T.T.Hang, “Invariant stable manifolds for partial functional differential equations with finite delay”. UTEHY Journal of Science and Technology, 2024, 41, pp. 65-70.